Mathematics, Neuroscience, and Epilepsy

BU mathematician Mark Kramer is building mathematical models of brain patterns that could lead to a better understanding of how the brain works, both in health and in the case of disease, such as epilepsy. Photo by Cydney Scott

Pulsars are the lighthouses of the universe, periodically shooting beams of radio waves outwards as they spin. As an undergraduate, Boston University mathematician Mark Kramer found himself studying these stars. He liked math and he liked applying it to real-world problems, even those involving objects light-years away.

Kramer, now an associate professor in the BU College of Arts & Sciences (CAS) Department of Mathematics & Statistics, still loves using math to solve tangible issues, but these days he focuses on questions closer to home. Much closer. He studies brains. Particularly, he studies rhythmic pulses of electricity that allow communication across the brain’s centimeter-scale universe.

Kramer’s work, which concentrates on mathematical modeling of epileptic seizures, is giving neurologists new insights into ways to help patients with intractable epilepsy by identifying the patterns present in the brain before, during, and after a seizure. It is also giving rise to never-before-seen mathematics, in the form of equations that behave in unexpected, counterintuitive ways even though they are based on the normal firing patterns of neurons. His approach—at once hands-on, through close collaboration with clinicians and other mathematicians, and distanced, with a keen eye for elegance and simplicity in his models—is building the foundation for a more streamlined and computationally powerful era of mathematical neuroscience.

Finding Neuroscience

After completing an undergraduate degree at Oberlin College in 2001, Kramer decided to attend the University of California, Berkeley. He completed a doctoral degree in applied physics, with an initial focus on astrophysics. But the post-9/11 economic downturn in fall 2001 put funding in question. “I had to start thinking practically,” says Kramer.

It wasn’t practical thinking that got Kramer interested in neuroscience and epilepsy, though. It was a party. He started chatting with a researcher who was stumped by his own data, recordings of brain patterns produced from patients with epilepsy. Kramer offered to help and soon joined the same lab.

A few years later, in 2005, his doctoral thesis described a mathematical model of epileptic seizures that pointed to possible opportunities for therapeutic intervention to stop or control seizures. That early model did not result in new treatments, but it did provide the seeds for Kramer’s present work. His current models, combined with clinical observations of human seizures, could point to which biological mechanisms in a particular patient, or which mechanisms in patients in general, give rise to seizures, potentially giving neurologists clues as to where and how to intervene surgically or with medication.

Epileptic seizures vary in length, duration, severity, and also in how they affect the person experiencing them. While most people with epilepsy can control their seizures with medication or surgery, about thirty percent of people with the disease have a form that resists control. It is these patients that Kramer’s work focuses on. He works with data recorded from brains, much the way he worked with signals observed from stars. “I was used to looking for rhythmic activity,” he says. “So the transition was somewhat natural. But the brain is complicated. It’s a lot noisier, and a lot less understood.”

The brain produces electrical signals on several levels. At the finest scale, individual neurons fire, producing an electrical pulse called an action potential to send a signal to a nearby neuron. To measure these, an electrode must be inserted into the neuron to measure the voltage change as the neuron fires. These types of recordings are typically done only in animals because they are so invasive.

At a much broader scale—the scale Kramer’s early model of epilepsy focused on—thousands of neurons collectively produce electrical pulses that course throughout the brain. These signals, called brain rhythms, can’t easily be traced back to the neurons that produce them. But they can be easily detected because they travel through the skull and can be picked up by electrodes on the scalp using electroencephalography (EEG). EEG recordings capture rhythmic pulses such as slow pulsing alpha rhythms seen during rest, and beta rhythms, about twice as fast and associated with motor and other functions.

For patients with intractable epilepsy, clinicians may also use an invasive version of the EEG called an electrocorticogram (ECoG) to record brain rhythms. The procedure requires removal of a portion of the skull so that electrodes can be placed directly on the brain’s surface. ECoG produces more precise recordings that may help doctors pinpoint the source of the seizures and, if necessary, remove it surgically. Only patients with the most intractable epilepsy undergo ECoG recordings. After implantation, patients sit in the hospital for days-long recording sessions that capture the seizures they experience.

Today, to get access to this kind of data and interpret it intelligently, Kramer collaborates closely with clinicians, such as Sydney Cash, a neurologist specializing in epilepsy care at Massachusetts General Hospital. The models Kramer builds based on this data are designed to help Cash find new and better ways to help his patients. “These models are instrumental in allowing us to understand our data better and derive new, testable hypotheses about how the brain functions and does not function in epilepsy,” says Cash. “We are hoping that the modeling will help us create novel approaches to predicting which brain regions need to be altered to control a patient’s seizures.”

From New Models to New Math

When Kramer finished his doctoral degree in 2005, he wanted to learn more about how to build models from brain data. His advisors pointed him to BU and Nancy Kopell, a CAS professor of mathematics & statistics. BU has a history of mixing math with neuroscience that stretches back to the 1970s and Kopell, who is co-director of the Center for Computational Neuroscience & Neural Technology (CompNet), has been using mathematics to model the dynamics of the brain for several decades.

Kopell’s work at that time was focused on modeling local brain behavior, such as the firing of individual neurons or groups of connected neurons. Her mathematical models were directly connected to real biological structures, while Kramer’s models so far had been more abstract, not easily traced back to their physical source. Since the biology of individual neurons is better understood, the math in the model can be based directly on the ion channels and other physiological features that make the neuron fire. “Mark came to me because he wanted to fill in the blanks he had in terms of biophysical modeling experience,” says Kopell. “He turned out to be absolutely terrific at it.”

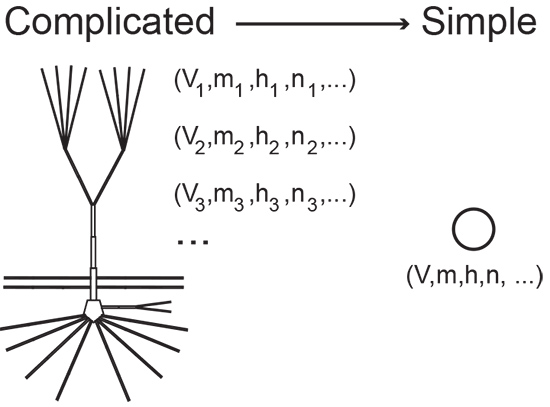
Mathematical models, like other kinds of models, aim to provide a simplified replica of a complex entity. A stick figure is a model of a human body, for example, and can be as evocative as it is unadorned. “Every model is imperfect,” says Grant Fiddyment, a neuroscience graduate student in Kramer’s lab. “It’s a cartoon.”

Mathematical models are often made of equations. For instance, an equation describing a line provides a rough model of the distance traveled over time by a runner in a race. A more complex model might track pace changes during the race and factor in respiration, metabolism, fuel intake, and so on. The model’s equations quickly become complicated. In fact, they can be so involved that they are incomprehensible, even for mathematicians.

The trick—and what sets Kramer apart—is knowing where to stop. “What Mark is really good at is staying grounded,” says Fiddyment. “He cuts through layers of complicated stuff and comes away with interesting but realistic models.”

In one instance, Kramer’s knack for building elegant models gave rise to new mathematics. The equations he developed behaved in a way that had never been seen before. “It was very interesting mathematics,” says Kopell. “And it was wholly unexpected.”

Kopell and Kramer had decided to look at an extremely complicated model of the neural-firing dynamics of Purkinje cells, large neurons in the brain that exhibit a firing pattern that includes bursts of electrical activity that sometimes transition into continuous spikes. The transition is marked by dynamics so complex that one model, which had been developed by other researchers, included 6,000 variables.

Kramer took an alternate approach. He started with a simpler model of the firing of a Purkinje cell—and also the oldest, the Hodgkin-Huxley model, equations written in 1952 that for the first time described the electrical signal that occurs when a neuron fires. “The Hodgkin-Huxley model is probably one of the best examples of interdisciplinary research in mathematical neuroscience,” says Kramer.

He layered on a few key variables to create a set of equations that describe voltage changes in the neuron and define the states the system enters and the trajectories it follows over time. Then he and Kopell studied the dynamics. That is, they studied the way solutions to the equations move in space, the same way a line modeling a runner in a race goes up and to the right on an X-Y axis, only—you guessed it—more complicated.

In these types of mathematical models, simply speaking, a system tends to move toward “attractors” and away from “repellors,” the same way a ball tends to roll downhill rather than up. But Kramer’s equations at times did the opposite, “which is weird,” he says.

The model is now in the hands of Kramer’s more abstractly focused colleagues in the mathematics department, showing the power of Kramer’s work to have wide influence. “We can use math to advance ideas in neuroscience, but we can also use the things we see in neuroscience to motivate ideas in math,” says Kramer.

Wait. What Is Mathematical Modeling, Again?

The concept of a mathematical model may still be hazy for the non-mathematician. It turns out that it isn’t so clear for mathematicians, either. They don’t always agree on what a model is or how to go about making one.

Kramer learned this firsthand when he joined the BU faculty in 2009. He teamed up with Uri Eden, a CAS associate professor of statistics, and started modeling epilepsy data again. The two had to learn how to communicate with one another about their different approaches to modeling. “Even though we were in the same department, crossing that boundary took awhile,” Kramer says.

To model whole-brain rhythms in epilepsy, Kramer uses a field of mathematics called graph theory to make network models. Network models are made of nodes and edges and look a bit like airline routes in the back of in-flight magazines. These types of models are used in studies of social media connections, connections between devices on the internet, and traffic patterns, like rush hour or air traffic. They fit naturally to rhythmic brain data because the rhythms link brain regions in a crisscrossed lattice of short-lived connections.

Network models differ from the dynamical systems modeling that Kramer practiced with Kopell. Dynamical systems models often spring from observations of concrete physical objects and measures that motivate equations describing how a system changes over time and in response to input. Scientists use dynamical systems to model natural systems, from climate change to firing neurons, and engineered systems, such as the vibrations of airplane wings.

Modeling has yet another meaning for statisticians like Eden. A statistical model of brain patterns recorded during a seizure might focus more on filtering out information that is less likely to be relevant to the seizure and bringing forward the sizes and shapes of the relevant signals.

A major focus of Kramer and Eden’s work is to figure out how to combine multiple modeling methods to get the most out of the data they get from their clinical collaborators. They are working closely with clinicians, like Cash, to bring together the expertise needed to develop automated computational modeling methods specifically designed for neuroscience. “What Mark and his group are doing is at the cutting edge of neuroscience,” says Cash.

Putting Models to Work

Kramer’s current work still involves parsing ECoG recordings from patients with intractable epilepsy. But now, in a project with Fiddyment, he is working with recordings at multiple spatial scales, from the level of rhythmic signals to those made by individual neurons.

His earlier data sets were produced by an 8×8 centimeter array of electrodes that picks up rhythmic signals from the surface of the brain. Kramer, Eden, Cash, and other collaborators at BU and Massachusetts General Hospital used this data to build a network model of a seizure in 2010. The model showed that the beginnings and endings of seizures are marked by massive cross talk, with almost every point in the network connecting with every other at the same time. Normally, just a few points connect, fleetingly, as needed to complete a cognitive task.

The new recording method adds a tiny 4×4 millimeter grid of microelectrodes at one location, typically close to the area of the brain where the seizure begins. This microelectrode array contains 96 channels that record the activity of individual neurons in that small region. The goal is to link this small-scale behavior with the large-scale patterns known to correspond with different phases of the seizure. “The overall concept of bridging information across widely separated scales is a major problem and challenge in the neurosciences,” says Cash. “These are very difficult problems to solve but doing so is key to our true understanding of brain activity.”

The modeling process is interactive and requires frequent check-ins with Cash. “It’s really easy to believe your model is true,” says Fiddyment. “So we regularly meet with clinicians to get their take. They help us see when our ideas are vague or ill-formed.”

Kramer’s ultimate goal in this line of research, which is funded by the Burroughs Wellcome Fund, the National Institutes of Health, and the National Science Foundation, is to both identify indicators of disease that can be easily detected and to propose possible biological mechanisms that underlie these indicators. For instance, Kramer’s models could provide a means of pinpointing which brain regions and biological mechanisms need to be altered through surgical removal, electrical stimulation, or medication to control seizures.

Kramer is also beginning to look beyond epilepsy. Valuable brain data from patients with different diseases and from healthy brains are also crossing his desk. “We’re thinking about all of it,” he says. “That’s the strength of mathematics. It can be applied anywhere.”